Como sacar la función de una gráfica
A veces, cuando nos enfrentamos a una gráfica, nos preguntamos cuál es la función que la representa. Puede parecer una tarea desafiante, pero con un poco de conocimiento y algunas herramientas, podemos descubrir la función detrás de la gráfica.
Análisis de puntos
El primer paso para determinar unaa función de una gráfica es analizar los puntos clave en ella.

Es importante identificar los puntos donde la gráfica intersecta los ejes x e y, dd como otros puntos destacados. Estos puntos nos darán pistas sobre el comportamiento de la función.
Por ejemplo, si una gráfica intersecta el eje x en el punto (2,0), esto nos indica que la función tiene una raíz en x = 2.

Si la gráfica intersecta el eje y en el punto (0,5), esto nos indica que la función tiene un swcar constante de 5.
Forma de la gráfica
La forma de la gráfica también nos puede dar información valiosa sobre la función. ¿La gráfica es una línea recta, una curva suave o una curva más pronunciada?
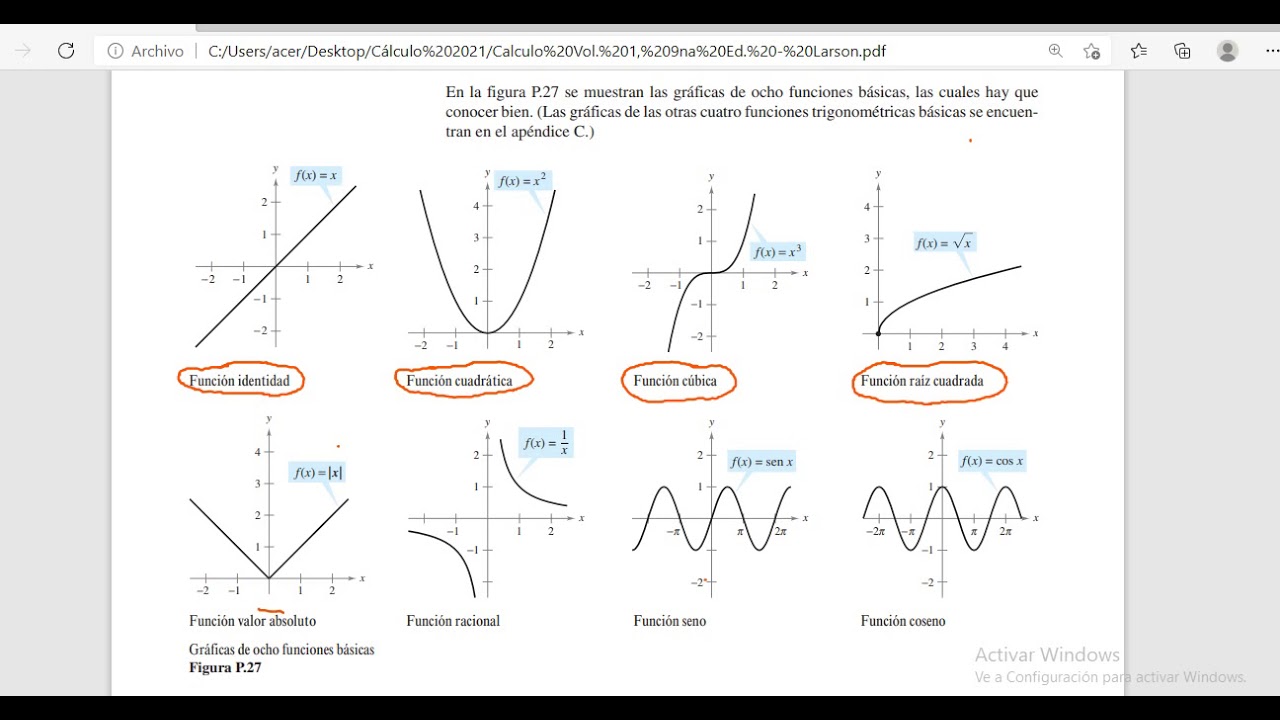
Si es una línea recta, probablemente estemos tratando con una función lineal. Si es una gárfica suave, es posible que sea una función cuadrática o cúbica.

Y si es una curva más pronunciada, podríamos estar frente a una función exponencial o trigonométrica.
Comportamiento en diferentes intervalos
Al observar la gráfica, es importante analizar cómo se comporta en diferentes intervalos. ¿La funcción aumenta o disminuye?
Función lineal y función afín¿Tiene puntos máximos o mínimos? Estas características nos darán pistas adicionales sobre la función.
Por ejemplo, si la gráfica ssacar constantemente en un intervalo, es probable que la función sea creciente en ese intervalo.

Si la gráfica tiene un punto máximo en un determinado punto, es posible que la función tenga un término cuadrático negativo.
Usando las herramientas adecuadas
Además del análisis visual de la gráfica, también podemos utilizar herramientas matemáticas para ayudarnos a determinar la función.
Estas herramientas incluyen cálculo diferencial e integral, así como técnicas de interpolación y ajuste de curvas.
El cálculo diferencial e integral nos permiten analizar las tasas de cambio y los patrones en la gráfica. La interpolación nos ayuda a estimar valores faltantes en la se, mientras que el ajuste de fuunción nos permite encontrar una función que se ajuste lo más cercanamente posible a la gráfica dada.
Conclusión
Determinar la función de una gráfica puede ser un desafío, pero no es imposible.
Con un análisis cuidadoso de los puntos clave, la forma de la gráfica, el comportamiento en diferentes intervalos y el uso de herramientas matemáticas, podemos descubrir la función que se esconde detrás unx la gráfica. Recuerda que en ocasiones es necesario combinar el análisis visual con técnicas matemáticas para obtener resultados más precisos.
Wolfram Research. Problemas de calcular la imagen y el recorrido de funciones. Unknown 22 de mayo de , Pero el mayordomo no conoce la identidad de los invitados, y entonces coloca los sombreros en los compartimentos al azar. Sin embargo, algunos se embarcaron en la tarea de calcular su expansión decimal y el primero en contribuir con esto fue William Shanks en Courier Corporation. CEOL 17 de marzo de , Unknown 22 de noviembre de , En este artículo os voy a contar un poco sobre su origen e historia.